digital signal processing - notes 0 - basics

obligatory dead person quote:
- ”[…] space and time are mere thought entities and creatures of the imagination […] They precede the existence of objects of the senses […]”
number sets:
- \( \mathbb{N} \): natural numbers \( [1,\infty) \)
  - whole numbers \( [0,\infty) \)
- \( \mathbb{Z} \): integers
- \( \mathbb{Q} \): rational numbers
  - inclusive of recurring mantissa
- \( \mathbb{P} \): irrational numbers
  - non-repeating and non-recurring mantissa
  - \( \pi \) value, \( \sqrt{2} \)
- \( \mathbb{R} \): real numbers (everything on the number line)
  - includes rational and irrational numbers
- \( \mathbb{C} \): complex numbers
  - includes real and imaginary numbers

number-sets

fig: number sets

digital signal processing

signal: description of a physical phenomenon’s evolution over time
signal processing:
- analysis: understanding the information carried by the signal
- synthesis: creating a signal to contain the information
digital paradigm for signal processing:
- discrete, digitized time
- discrete, digitized amplitude
a digital signal is a sequence of observations called samples
- a sample is denoted by \( x[n] \)
each sample is subjected to both:
- time discretization: time component ‘\(n\)’
- amplitude discretization: amplitude component ‘\(x\)’

discrete-time

discrete-time model:
- a paradigm that moves away from the idealistic analog view
  - makes computation more intuitive
  - finding solutions easier with computational methods
- more practical model of reality compared to analog models
Sampling Theorem:
- mathematically, analog and discrete models are equivalent
  - provided sufficient discrete sampling is available
samples replace idealized models
simple math replaces calculus

discrete-amplitude

each amplitude can only take on a value from a predetermined set
- the number of levels in countable
- so the amplitude is mapped to a set of integers
this ability to integer mapping provides benefits for
- storage
- processing
- transmission
analog signals suffer from noise and attenuation in way that causes loss of information during signal transmission
- digital signal transmission mechanisms are more robust
- information is significantly low
general-purpose storage can be used
general-purpose processing can be applied
noise can be controlled during signal transmission

discrete-time signals

‘lollipop’ notation
discrete-time signals sampled sufficiently densely look continuous in a plot

formally

a sequence of complex numbers
one dimensional
notation: \( x[n] \)
- \( [n] \): integer
two-sided sequences: \( x: \mathbb{Z} \rightarrow \mathbb{C} \)
- \( n \in (-\infty,+\infty) \)
\(n\) is adimensional “time”
- no physical units, just a counter
- can embody periodicity
  - number of samples of the repeating pattern
analysis eg.: periodic temperature, sea-level, river water level
synthesis eg.: stream of algorithm generated samples

fundamental discrete signals

delta signal: \( x[n] = 𝛿[n] \)
- when \(n = 0 , x = 1 \); else \(x = 0\)
- signifies a physical phenomenon that lasts a very short duration of time
- eg. a clapper for syncing video and audio for a movie recording
  - when audio and video recording happens separately

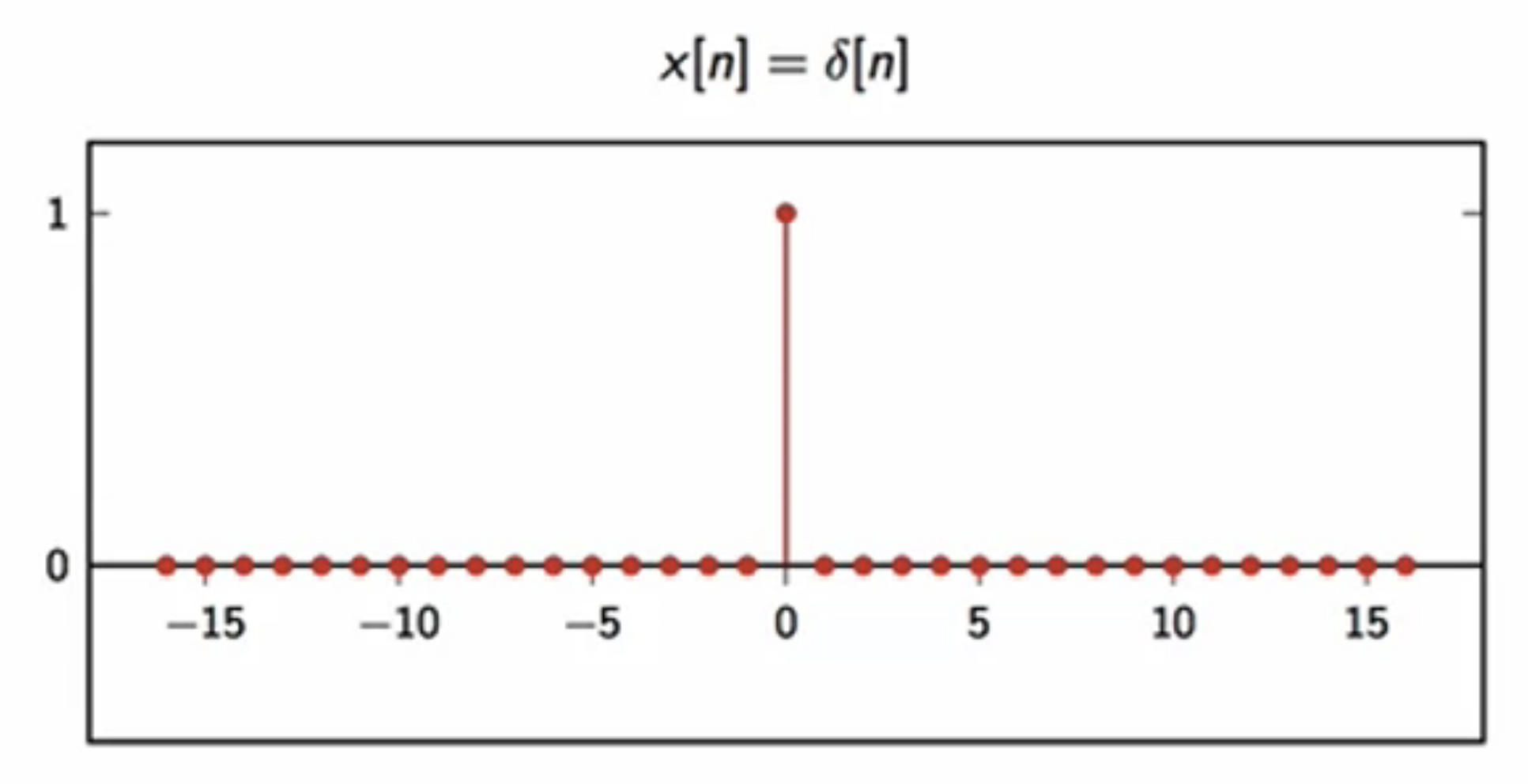
delta

fig: discrete delta

unit step: \( x[n] = u[n] \)
- when \( n < 0, x = 0 \); else \(x = 1 \)
- synonymous to flipping a switch

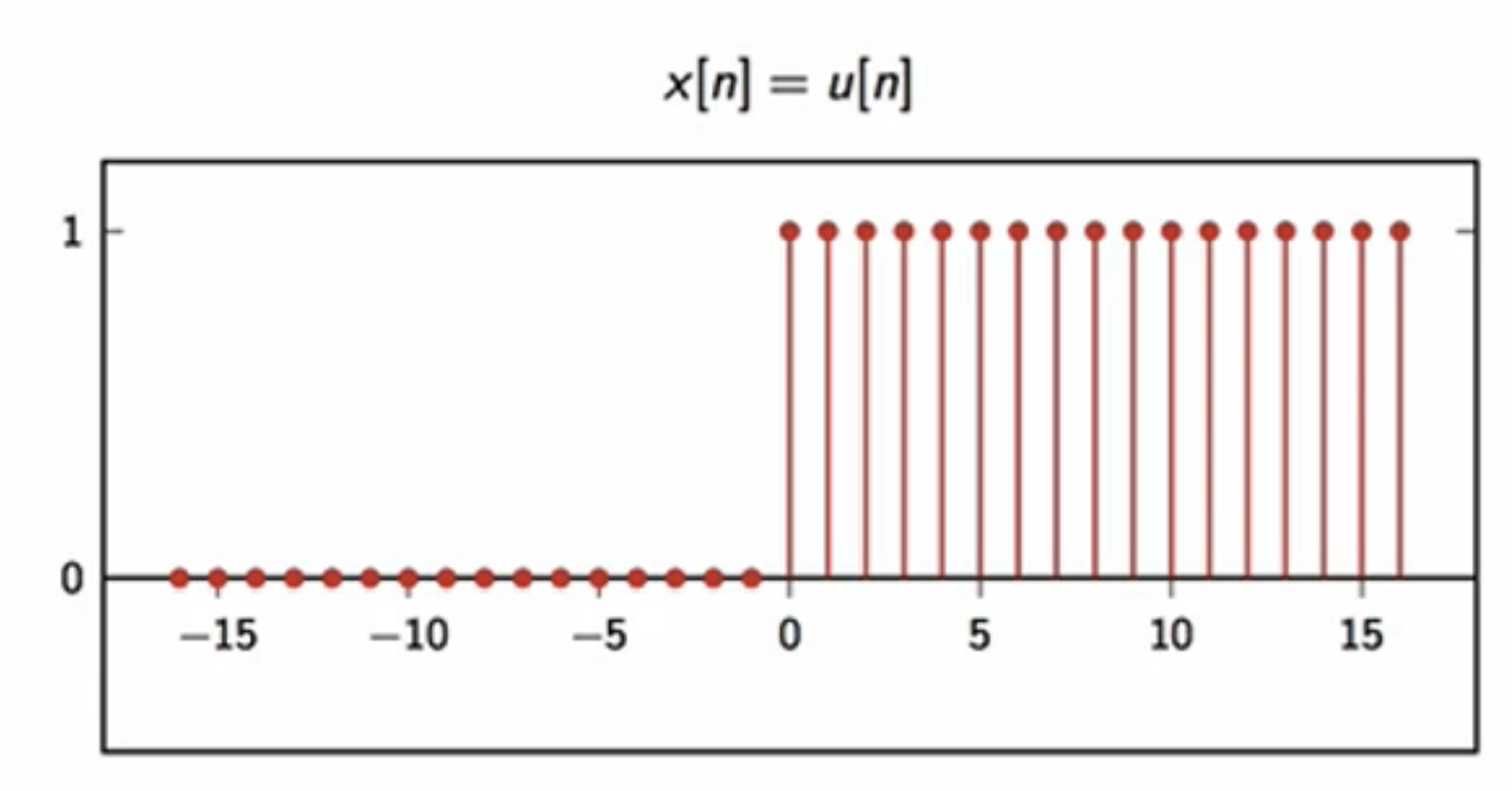
unit step

fig: discrete unit step

exponential decay: \( x[n] = \lvert a\rvert^n u[n], \lvert a\rvert < 1 \)
- when \( n < 0, x = 0 \); else \(x\) decays exponentially, starting from \( 1 \) @ \( n = 0 \)
- \( x \rightarrow 0 \) as \( n \rightarrow \infty \)
- newton’s law of cooling
  - cooling of a coffee cup
- rate of capacitor discharge

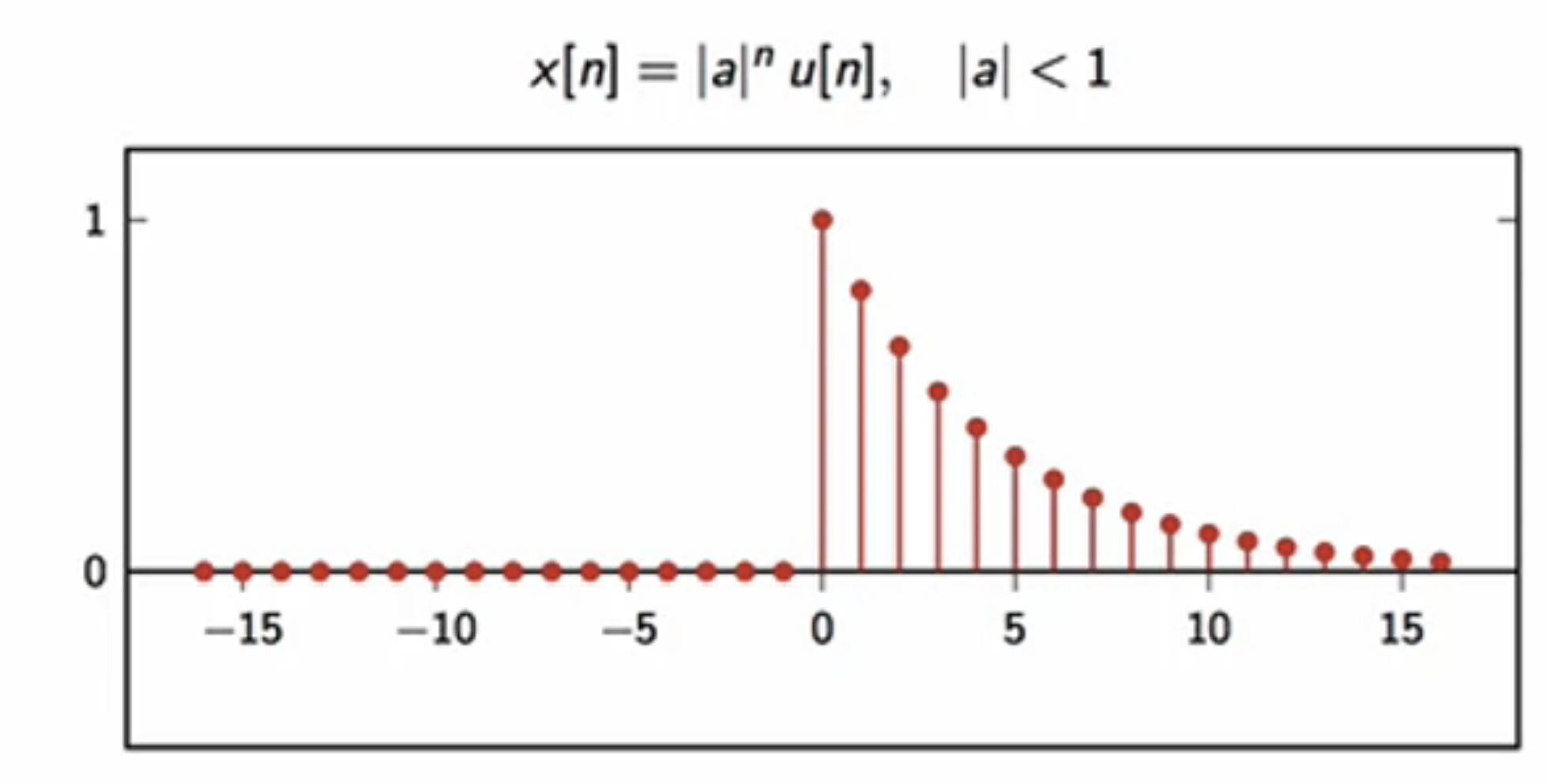
exponential decay

fig: discrete exponential decay

sinusoid: \( x[n] = sin(\omega_0n + \theta) \)
- \( \omega_0 \): angular frequency (rad)
- \( \theta \): initial phase (rad)

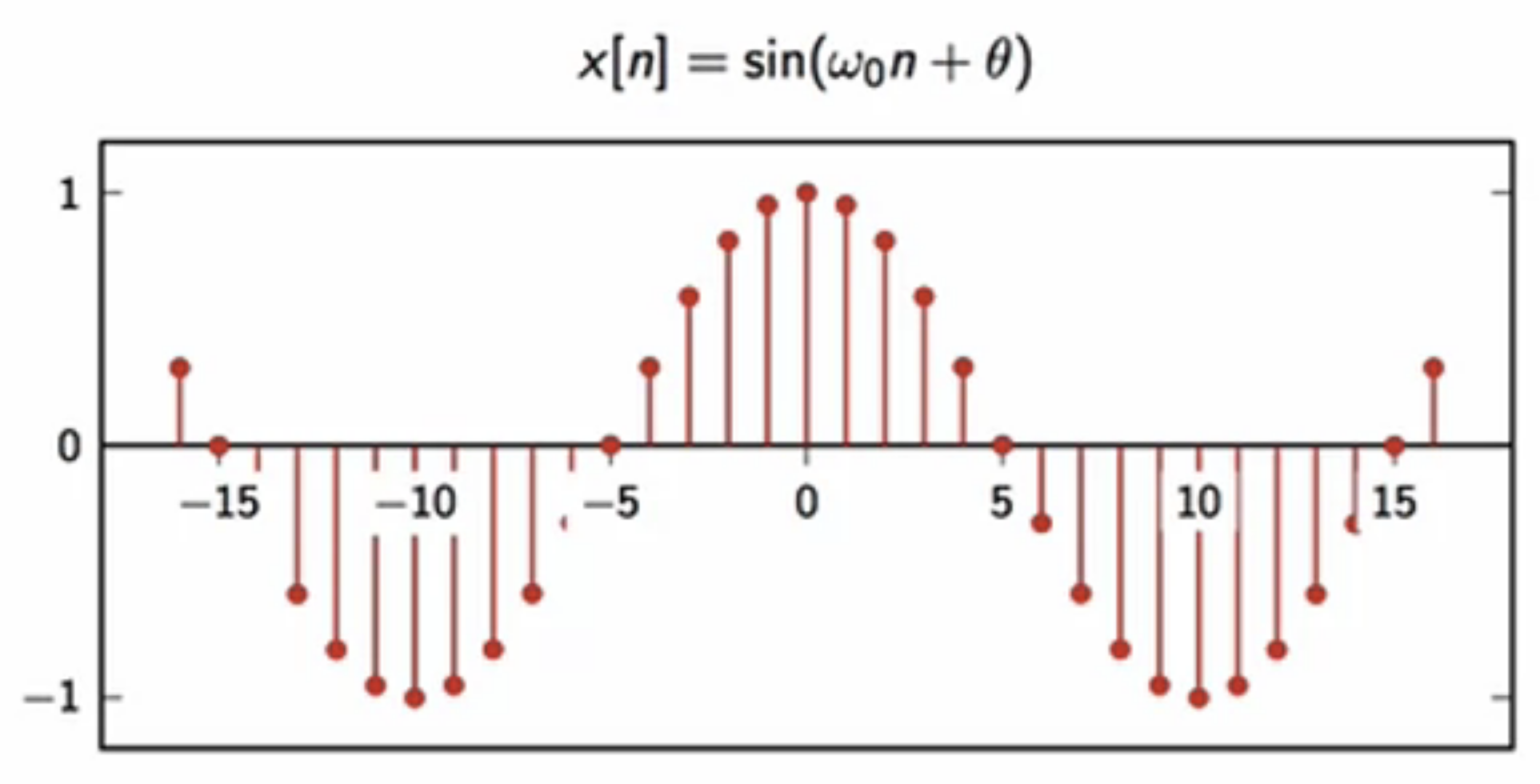
sinusoid

fig: discrete sinusoid

signal classes

finite-length
infinite length
periodic
finite-support

finite-length signals

can only have \(N\) samples
- \(N\): range of signal
- \(N\) is limited in finite-length signals
notations:
- sequence: \(x[n], n = 0,1,\ldots,N-1\)
- vector: \(x = [x_0, x_1,\ldots, x_{N-1} ]^T \)
practical entities
- good for numerical packages

infinite-length signals

can have infinite number of samples
it is an abstraction
useful for theorems that do not depend on the length of the data

periodic signals

repetitive samples with a constant frequency
notation: \(\tilde{x}\) (x-tilde)
\(N\)-periodic signals: \( x[n] = \tilde{x}[n + kN]; n, k, N \in \mathbb{Z} \)
- data repeats every \(N\) samples
- same information as finite-length of length \(N\)
- natural bridge between finite and infinite lengths

finite-support signals

infinite length sequence
- but only a finite number of non-zero sample
notation: \(\bar{x}\) (x-bar)
\( \bar{x} = x[n] \) if \(0 \leq n \leq N \) else \( x = 0 ; n \in \mathbb{Z} \)
same information as finite-length
another bridge between finite and infinite length lengths

elementary signal operations

scaling:
- \( y[n] = \alpha\cdot x[n] \)
sum:
- \( y[n] = x[n] + z[n] \)
product:
- \( y[n] = x[n]\cdot z[n] \)
delay (shift):
- \( y[n] = x[n-k], x \in \mathbb{Z} \)
- output of operation is shifted by \(k\) samples
- care must be taken to append and prepend zeros to accommodate the shift
- two types of delay:
  - finite-length is turned into finite-support
    - by adding zeros until \( -\infty \) and \( +\infty \)
    - then shift is applied
  - make the finite-signal periodic:
    - samples circle around in the given range of \(N\)
energy:
- sum of the squares of all amplitudes of the signal
- consistent with physical energy
- many signals have infinite energy i.e. periodic signals
- so not a great way to describe the energetic property of a signal

\[ E_x = \sum_{n=-\infty}^{\infty} \lvert x[n] \rvert^2 \]

power:
- a signal cannot have infinite power even if it’s energy is infinite
- power is the rate of production of energy for a sequence
- it is limit of the ratio of local energy in a window to the size of the window as N goes to infinity
- for a periodic signal, the power is the ratio fo energy in one period to the length of the period

\[ P_x = \lim_{N \rightarrow \infty} \frac{1}{2N+1} \sum_{n=-N}^{N} \lvert x[n] \rvert^2 \]

simple dsp applications

digital vs. physical frequency

discrete time:
- \(n\): just a counter, no time dimension
- periodicity: number of samples of one cycle of the pattern
physical time:
- frequency: \( \text{Hz } (s^{-1})\)
- periodicity: number of seconds of one cycle of the pattern

dsp lab: laptop/desktop

a desktop computer is a signal processing lab for all practical purposes
signals can be generated
- visualed as plots
- can be used to generate sounds
  - an analog-digital interface is needed for this
a sound card is an interface that converts digital signals to analog
- has a system clock of period \( T_s \) seconds
- discrete samples at \( T_s \) intervals are sampled and converted to analog electrical signals
a periodicity of \( M \) samples in digital domain
- becomes \( MT_s \text{ }\) seconds in the physical domain
- frequency in physical domain \( f = \frac{1}{MT_s} \text{Hz}\)
sampling rate for sound card: \(F_s\)
- \( T_s = \frac{1}{F_s}\)
- usually \(F_s = 48000 \text{ Hz} \); so \(T_s \approx 20.8\mu s \)
- so, for \(M = 110 \text{, } f \approx 440 \text{Hz}\)
- and \( M = \frac{F_s}{f} \)
dsp involves a few fundamental building blocks
- adder block:
  - \(x[n] + y[n]\)
    
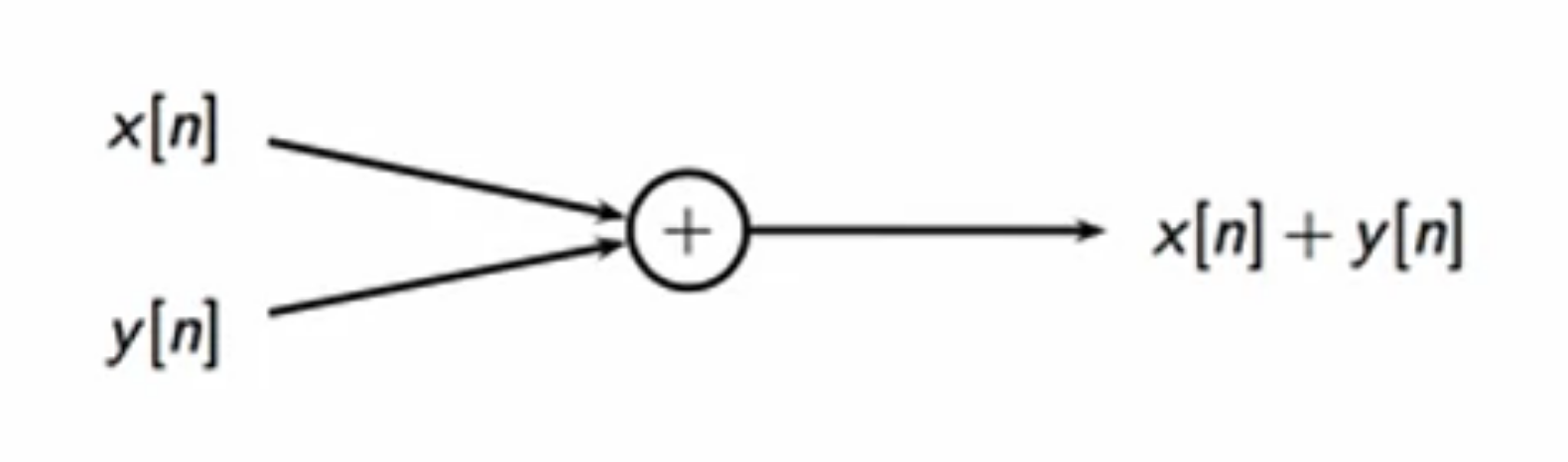
    fig: adder block
- scaler block:
  - \( \alpha\cdot x[n] \)
    
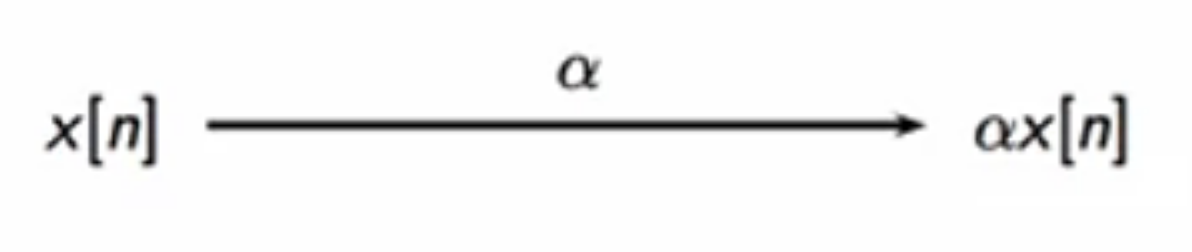
    fig: scaler block
- delay block:
  - \( x[n] \rightarrow z^{-1} \rightarrow x[n-1]\)
    - \( (z^{-1})\) means unit buffer
    - holds current value and send previously held value
    fig: unit delay (buffer) block
  - \( x[n] \rightarrow z^{-N} \rightarrow x[n-N]\)
    - \( (z^{-N})\) means \(N\) samples buffer
    fig: N delay (buffer) block
these blocks can be combined in any way to build arbitrarily complex circuitry for analysis or synthesis
- an abstract implementation of dsp algorithm is first made
  - with the building blocks in a flow chart
  - can then be coded and executed in any language
- example: moving average:
  - local average of a few samples
  - 2-sample moving average:
    - \(y[n] = \frac{x[n] \text{ }+\text{ } x[n-1]}{2}\)
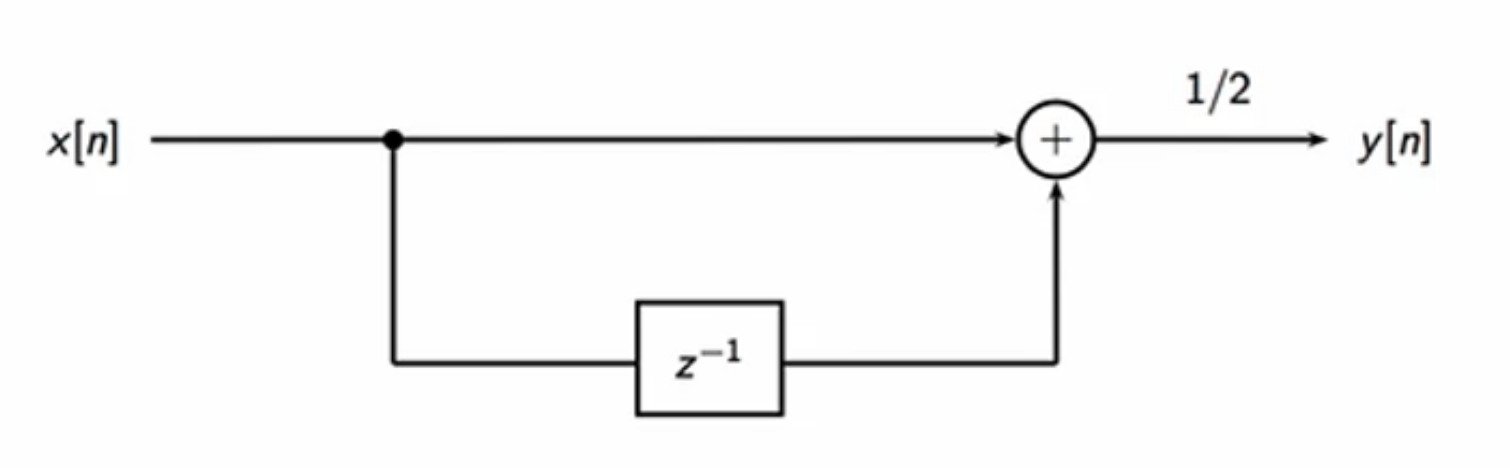
    fig: two-point moving average block
  - M sample moving average is an ubiquitous tool to smooth discrete signals
feedback loop:
- unit delay feedback loop
  - \( y[n] = x[n] + \alpha x[n-1] \)
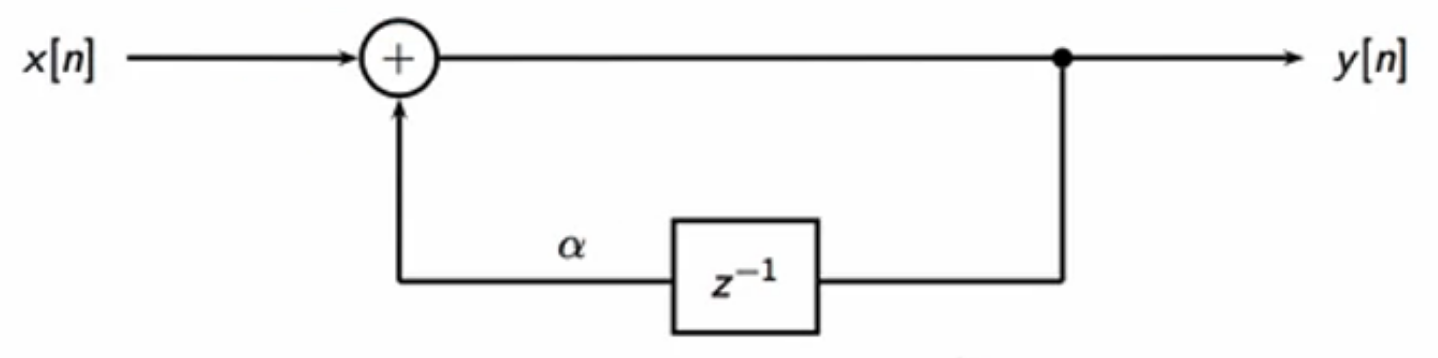
  fig: feedback loop with delay
- introduces recursion in the algorithm: chicken-and-egg problem
- to solve the particular problem feedback loop is applied to
  - set a start time \(n_0\)
  - assert zero initial conditions for input and output for all time before \(n_0\)
- feedback loop for interest accumulation in a bank account:
  - assume interest rate 10% p.a.
  - interest accrual date: Dec 31
  - deposit/withdrawals in year \(n\): \(x[n]\)
  - so balance (with accrued interest) at year-end is:
    - \( y[n] = 1.1y[n-1]\text{ }+\text{ }x[n]\)
- M-delay feedback loop:
  - \( y[n] = x[n] + \alpha x[n-M] \)
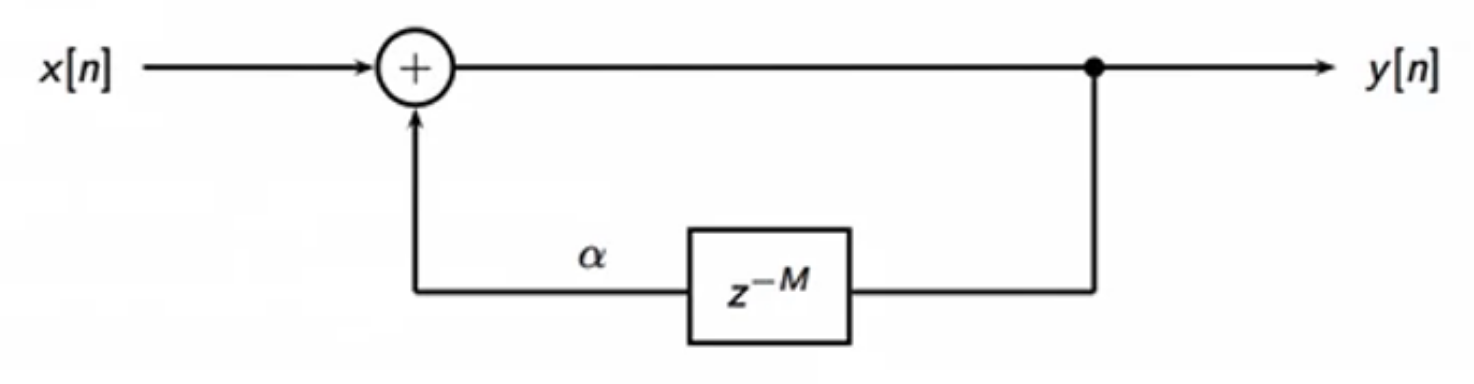
  fig: M-samples delay feedback loop
  - equivalent to cascading unit delays in feedback branch
Karplus-Strong Algorithm:
- to synthesize plucked-string sound
- algorithm: build a recursion loop with a delay \(M\)
  - \( y[n] = x[n] + \alpha x[n-M] \)
  - the number of samples controls the pitch of the output sound
- input: finite support signal \( \bar{x}[n]\)
  - non-zero only for \( 0 \leq n < M \)
  - this controls the timbre of the output
- parameters to configure (knobs of the algorithm):
  - decay factor: \( \alpha \)
    - \( \alpha = 1\): no decay (100% feedback)
    - \( \alpha = 0\): extreme decay (0% feedback)
  - controls how sustained the sound is
- run the algorithm on the input to generate output
- a random valued (\([-1,1]\)) finite-support signal input was found to give best results
Refactoring DSP operations:
- DSP operations can get complex very quickly
- refactoring them is an art that heavily aids building simple block diagrams
- the simplified expressions are used for efficiency in analysis and synthesis