oscillations

• oscillations are everywhere
• sustainable dynamic systems are always oscillatory
• things that don’t move in circles don’t last
  • bombs
  • rockets
  • human beings (only partially oscillatory)

clip: gyroscopic stability of a disc player in zero-gravity - OFF vs. ON

• an oscillation is cyclic, it goes around in circles
  • all oscillations can be described with a combination of cosine and sine functions

representing an oscillation

• a complex reference system centered on the origin of the oscillation is used for this
• a complex exponential is used to describe the position on the plane of oscillation
• \(x(t) = \exp(j\omega t)\), where \( \exp(j\omega t)\) is the complex exponential
  • \(j = \sqrt{-1}\)
  • \(\omega \): rotation/oscillation frequency
  • \(t\): physical domain time

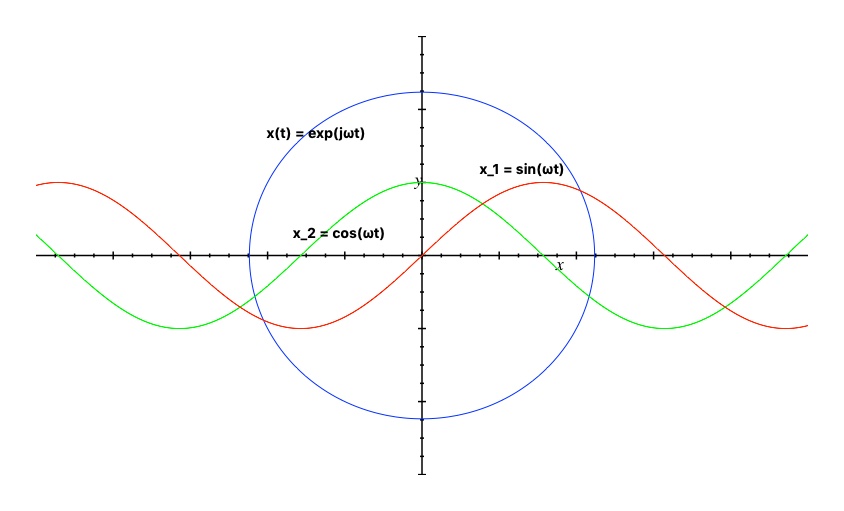
fig: complex exponential in complex plane with sin and cos functions

• trigonometric expansion of complex exponential:
  • \(x(t) = \exp(j\omega t) = \cos(\omega t) + j \sin(\omega t)\)
  • called euler’s formula

sample notation with complex exponential

• \(x[n]\): discretized sample notation
• complex exponential sample notation
  • \( x[n] = A\exp(j(\omega n + \phi)) \)
• trigonometric complex sample notation
  • \( x[n] = A [ \cos(\omega n + \phi) + j\sin(\omega n + \phi)] \)
• where:
  • \( \omega \): frequency (radians)
  • \( \phi \): initial phase (radians)
  • \( A \): amplitude
• note that phase and frequency are both in radians when using the complex exponential paradigm

---

complex exponential notation

justification for use in dsp

• every sinusoid can be written as a sum of the sine and cosine
  • sine and cosine live together
• trigonometry becomes algebra, so notation is simpler
  • helps avoiding the use of trigonometric identities
    • significantly reduces the number of terms in equations
  • phase can be managed with exponent summation and split rule
  • phase shifts are simple complex multiplications
• complex numbers can be used in digital systems without obstacles

anatomy of the complex exponential

• polar form of complex exponential:
  • \( e^{j \alpha} = \cos \alpha + j \sin \alpha \)

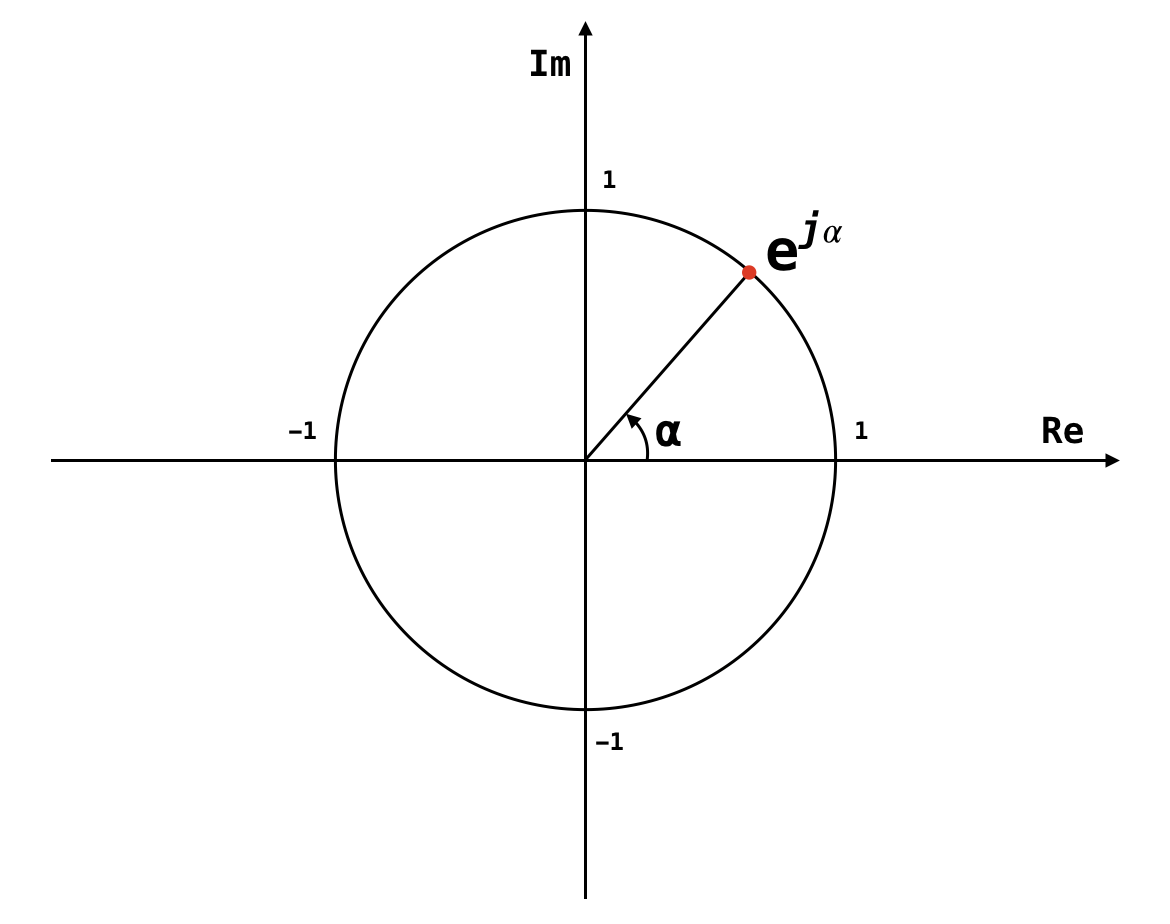
fig: \( e^{j \alpha}\) on the complex plane (argand diagram)

• \( e^{j \alpha} \) is a unit circle on the complex plane
  • unit circle: \( \lvert e^{j \alpha} \rvert = 1\)

rotation about the origin complex plane

• say \( z \) is a point on the complex plane
  • by multiplying it with \( e^{j \alpha} \)
  • \( z \) is rotated about the origin
    • in the anti-clockwise direction by amount \(\alpha\)
    • about the origin
    • with radius of rotation \( = \lvert z \rvert \)

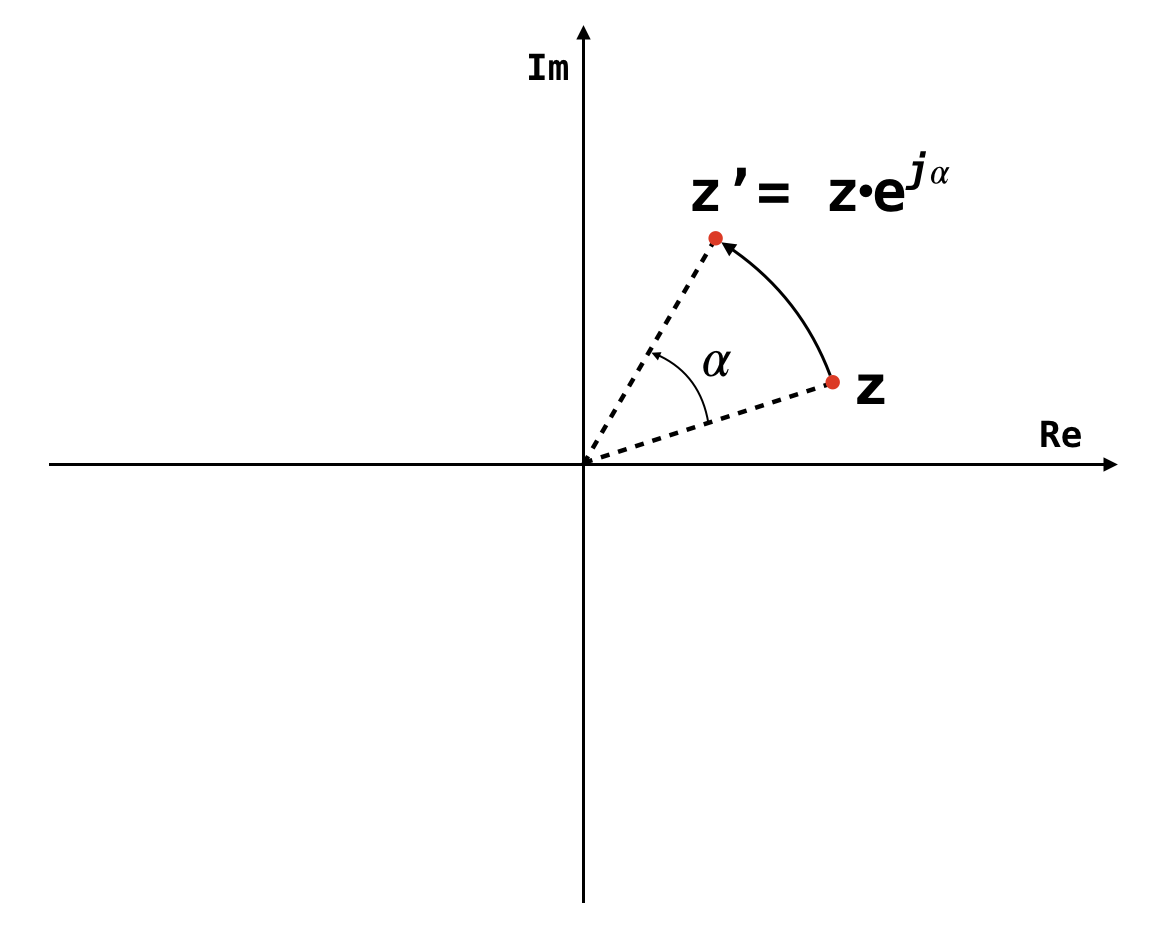
fig: rotation by multiplication with \( e^{j \alpha}\)

• this rotation operation is the basis of the complex exponential generating algorithm
  • used to synthesize signals
    • \(x[n] = e^{j \omega} \)
    • \(x[n+1] = e^{j \omega}x[n] \)
    • \(x[0] = 1\)
  • with an initial phase:
    • \(x[n] = e^{j \omega + \phi} \)
    • \(x[n+1] = e^{j \omega}x[n] \)
    • \(x[0] = e^{j \phi}\)
• in discrete time, a sinusoid \( e^{j\omega n} \) is periodic only if:
  • \(\omega = \frac{M}{N}2\pi\); \(M,N \in \mathbb{N}\)
  • i.e. only if:
    • frequency, \(\omega \), is a rational multiple of \( 2\pi \)
    • or equivalently, if \(e^{j\omega N} = 1\)
  • so not every sinusoid is periodic in discrete time

aliasing

• the same point in the unit circle may have many names:
  • the point at \(e^{j\alpha}\) can
    • \(e^{2\pi + j\alpha}\)
    • \(e^{6\pi + j\alpha}\)
    • \(e^{-2\pi + j\alpha}\)
• this is called aliasing
  • natural property of complex exponential

• in discrete time, this limits how fast we can go around the unit circle with a discrete-time signal

• the frequency of the discrete-time machine is limited
  • \(0 \leq \omega < 2\pi\)
  • when it is faster than \(2\pi\), due to the periodicity of the complex exponential,
    • we fall back via a modulo operation
• even within the range, care must be taken between backwards and forwards motion
  • when \(\omega = \pi \),
    • the point simply oscillates between \( 1 \) and \(-1\) on the unit circle
  • when \(\omega > \pi\)
    • it can also be view as rotation backwards to get that point
    • it is shorter to get to that point in the backwards direction
  • so anytime \(\omega > \pi\),
    • it appears like a smaller step in the clockwise direction
  • this reverse effect aliasing is even more pronounced when \(\omega\) is close to \(2\pi\)
  • if \(\omega » \pi \), the rotating body appears stationary due to aliasing
• so at different frequencies, i.e. \(\omega \) values, aliasing introduces different artifacts of illusion

---

eigenvalues and eigenvectors

• almost all vectors change direction when they are multiplied by a matrix
• however, certain vectors are in the same direction even after multiplication with that matrix
  • those certain vectors are eigenvectors
• since they are the in the same direction, multiplication with the matrix is like scaling the original vector
  • the equivalent scaling factors are called eigenvalues
• consider equation: \( Ax = \lambda x \)
  • \(A\): square matrix
  • \(\lambda\): eigenvalues of \(A\)
  • \(x\): eigenvectors of \(A\)
• rearranging this, we get: \( A - \lambda I = 0\)
  • from this we get A’s characteristic equation:
    • \(\lvert A - \lambda I \rvert = 0\)
    • where \(\lvert A \rvert\): determinant of matrix \(A\)
  • the roots of this equation are eigenvalues \(\lambda\)

• having computed the eigenvalues \(\lambda\), the eigenvectors \(x\) can be found using \( Ax = \lambda x \)

• if eigenvector elements can take on arbitrary values based on a relationship between them, make sure to normalize them with the square root of the sum of squares of all elements
  • i.e. normalize it with the length (first modulus) of the vector

---

references

• \(e^x \) vs. \( \exp(x) \)
• argand diagram

---