contents

• mp3
  • origins
  • lossy compression scheme
  • encoding
• mp3 encoding - block diagram
  • masking effect
  • psycho-acoustic model
  • sub-band filtering
  • quantization
  • mp3 performance
• references

---

mp3

• MP3:
  • stands for MPEG - Layer 3
  • MPEG: Motion Picture Expert Group

• in the 90’s a bunch of experts agreed on a set of standards for digital video and audio compression and encoding

• MP3 format of audio compression and encoding turned out to be the popular digital audio format for
  • streaming
  • storage
  • playback
• a portable music device can store up to 30000 mp3 files

fig: \(mp^3\) digital audio encoding

• various dsp tools come together to make this encoding possible

origins

• mp3 based on compression algorithms developed in the fraunhofer institutes in germany
• mp3 standard was quickly embraced in the industry
  • strong PR

lossy compression scheme

• start with a discrete-time sound signal \(x[n]\)
• goal:
  • reduce number of bits to represent original
  • reduce memory requirements to store sound signal

fig: digital signal flow - encoding and decoding

• \(x[n]\) is fed to an encoder where it is converted to a binary string
  • goal here is to reduce the memory required to store the waveform
• a decoder is designed to convert it back to a sound signal \(y[n]\)

encoding

• mp3 encoding reduces the number of bits needed for a digital sound signal by a large amount
  • the tradeoff is sound quality
  • the lesser size it is encoded to, more the sound degradation
  • so, mp3 encoding is a lossy compression scheme

storage size comparison

• consider a DVD standard audio file
  • this is uncompressed digital audio
  • sampling rate: 48 khz
  • digital bit depth: 16-bit per sample
  • takes 12 MB of storage for 1 min of stereo audio
• a high quality mp3 encoded takes
  • about 1.5 MB for the same 1 min stereo audio
  • this is about 10 times lesser than DVD quality
  • lossly digital audio file
  • sound quality degradation occurs, but usable

human ears and mp3

• key ingredient of mp3 encoding framework:
  • modelled around the human auditory system
• encoding doesn’t attempt to preserve the original structure of the input audio file
  • it focusses on encoding the most important parts of the input audio waveform
  • that are key to human ears listening to music and hearing sounds
  • the loss of the information form the original signal is placed in the spectrum that the human ear cannot hear

---

mp3 encoding - block diagram

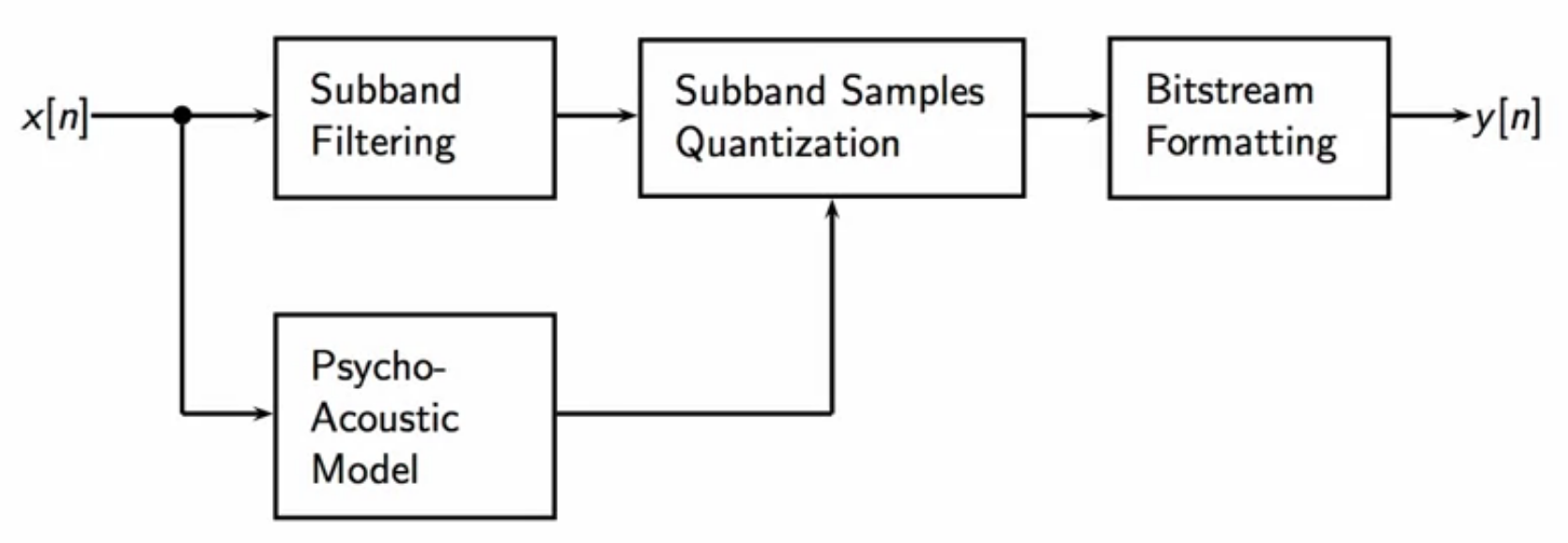
fig: mp3 encoding block diagram

• sub-band filtering: splits spectral range of input into 32 independent channels
• sub-band sample quantization: each channel is quantized independently
  • number of bits each allocated to each sub-band is dependent on the perceptual importance
  • sub-bands that are of not important and difficult to be perceived by the human ear are assigned very few bits or none at all
  • more perceptually relevant it is, the more of the bulk of the bit budget is allocated to that sub-band
  • this possible because of the masking effect of the human auditory system
• bit-stream formatting: quantized samples are formatted and encoded in a continuous bit stream

masking effect

• example of the masking effect:
  • in a quiet room, possibly at night, the human ear can even hear the ticking of a watch
  • in an environment with a lot of ambient noise, possibly in the day, the ear cannot hear the ticking of a watch
    • it is drowned out in the ambient noise of higher amplitudes
  • but an audio recording will contain the ticking watch information in both the quiet and the noisy environments
    • this can be seen in the audio recording spectrum
• for a given environment of sounds, there is a unique masking threshold
  • the shape of this masking threshold is determined experimentally
  • by running a lot of listening tests with human subjects

relative amplitudes

• consider a sound like below with a pronounced peak
  • the blue curve is the spectrum of the sound
  • the red dot is the strongest component
  • the red dotted line is a masking threshold

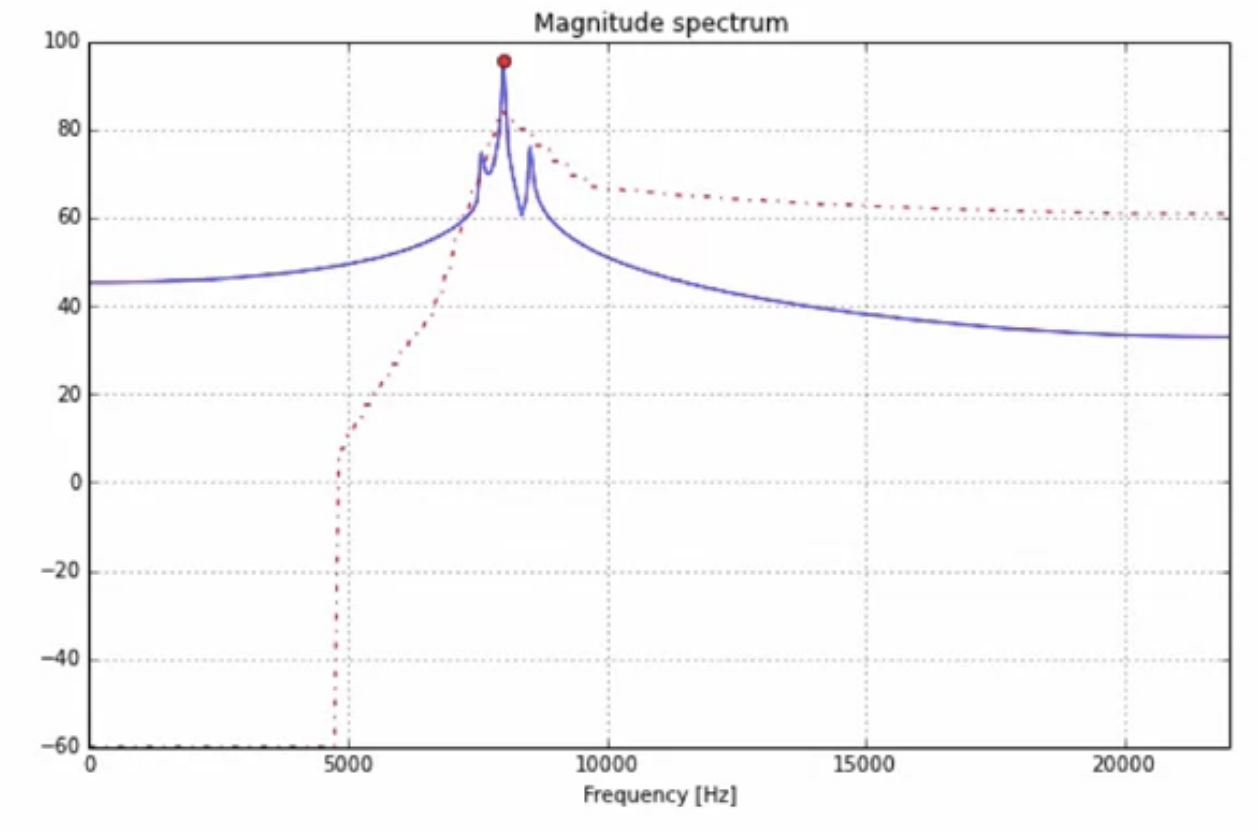
fig: masking effect of human auditory system

• a masking effect takes place in the the human ear for a sound like this
• the frequency components in the vicinity of the peak strength are not heard unless they are louder than a giving masking threshold
• anything below the red dotted line will not be heard by the ear
  • this can be removed without any perceived quality loss

frequency resolution

• masking in human ear takes place within critical bands
  • these critical bands are treated by human ear as a single unit
  • two different frequencies within a single band are perceived as one single tone
    • everything within a band can NOT be resolved further in the ear
  • there are around 24 bands critical bands for the human ear

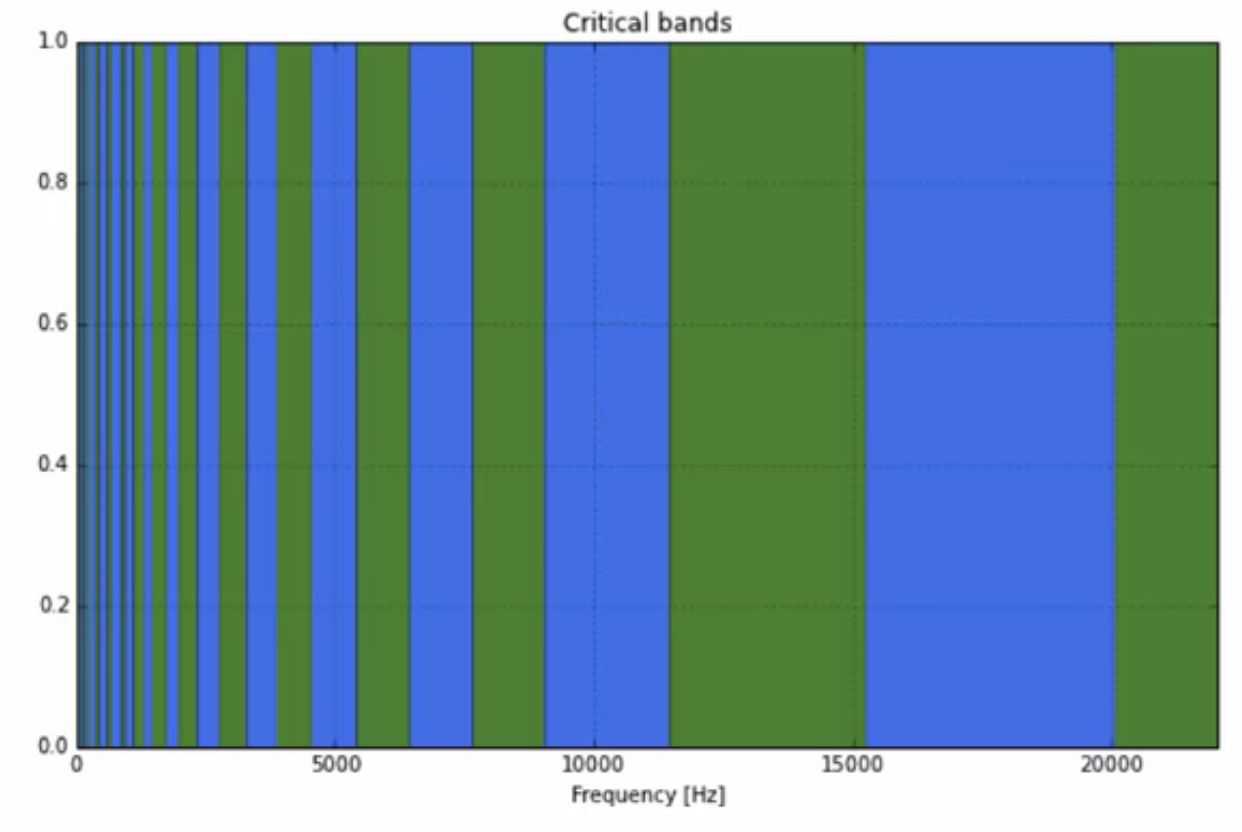
fig: frequency distribution of critical bands of human hearing

• the critical bands are not linearly distributed, it is logarithmic
  • the resolution power of the ear is higher at low frequencies
  • as the frequencies get higher, the resolution in the ear is less discriminant
• since the human ear is less discriminant in the higher frequencies
  • more noise is tolerated in the higher frequencies than in the lower frequencies
  • noise in the higher frequencies cannot be resolved by the human ear
• so, more masking in higher frequencies because of the logarithmic distribution of the critical bands

psycho-acoustic model

• this is the bit allocation procedure that assigns the number of bits to each of the 32 sub-bands

• auditory perception based bit allocation procedure

  • NOT uniform bit allocation

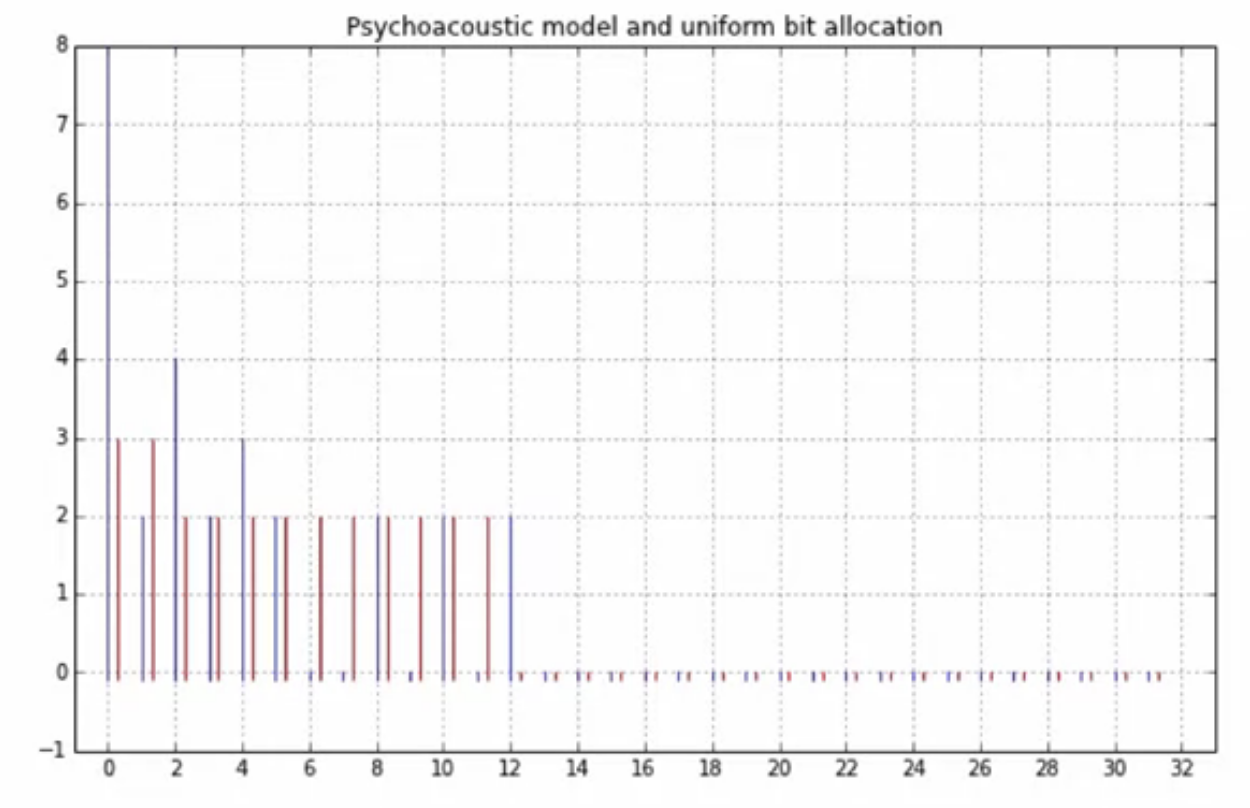
fig: psycho-acoustic vs. uniform bit allocation

• purpose of psycho-acoustic model
  • compute minimum number of bits for each of the 32 sub-bands in the mp3 encoding
  • such that perceptual distortion is minimized

• a non-uniform bit allocation is obtained which allocates fewer bits to bands with strong masking

• the psycho-acoustic model is not a part of the mp3 specification
  • it is continuously improved by tests and research
• the number of bits user of each sub-band is sent along with the quantized data
  • quantization is agnostic to the method of bit allocation
• this procedure is technically involved and has several steps, here is an outline

step 1

• use FFT to estimate the energy in each sub-band

step 2

• distinguish tonal (sine like) and non-tonal (noise like) components

step 3

• determine masking effect of tonal and non-tonal components in each critical band

step 4

• determine total masking effect by summing the individual contributions
  • obtain global masking curve

step 5

• map this total effect to the 32 sub-bands

step 6

• determine bit allocation by allocating polarity bits to aub-bands with lowest signal-to-mask ratio

sub-band filtering

• the input signal is fed to a filter bank
• filter bank has 32 filters, each extract one sub-band from input
  • isolates different parts of the spectrum

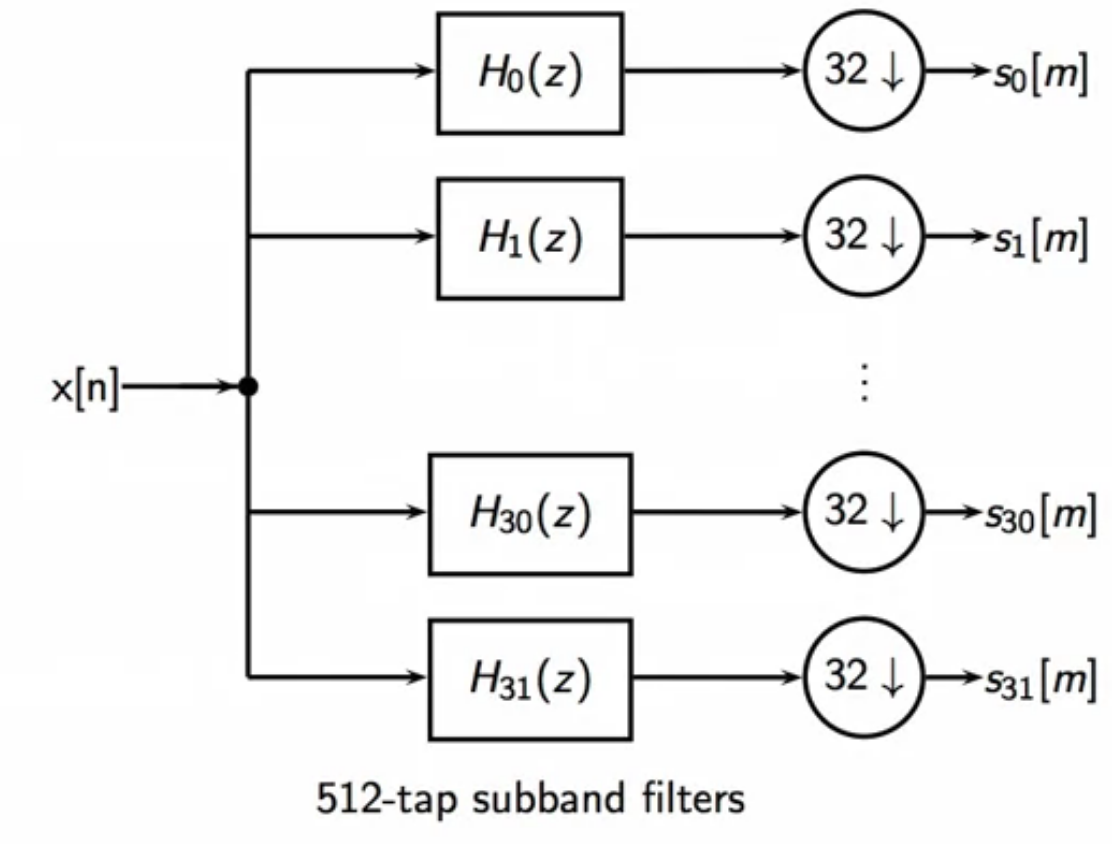
fig: sub-band filtering

• filters are 512-tap FIRs (Finite Impulse Response)
• each filter is followed by a 32X down-sampler
  • provides independence of band samples
• the prototype filter is lowpass filter with
  • a cutoff frequency of \( \frac{\pi}{64} \)
  • bandwidth of \( \frac{\pi}{32} \)

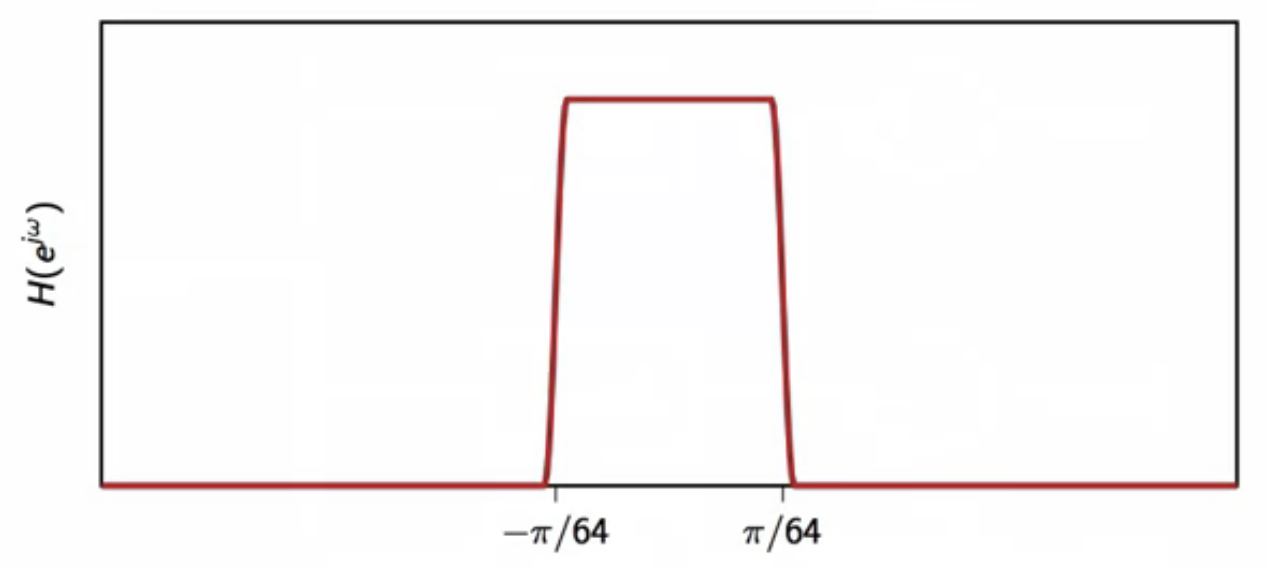
  fig: sub-band filter prototype - lowpass filter

• each base filter is modulated with a different cosine
  • below is the modulation for the i-th filter \[ h_i[n] = h[n]\cos\Big ( \frac{\pi}{64} (2i + 1)(n - 16) \Big ) \]
  • at multiples of \( \frac{\pi}{64} \)
• after modulation, each filter lets through a fraction of the 32 splits of the input spectrum as shown below
  • there is no overlapping between the parts of spectrum let through by the filters
  • the 32 spilts are spread over the entire specturm

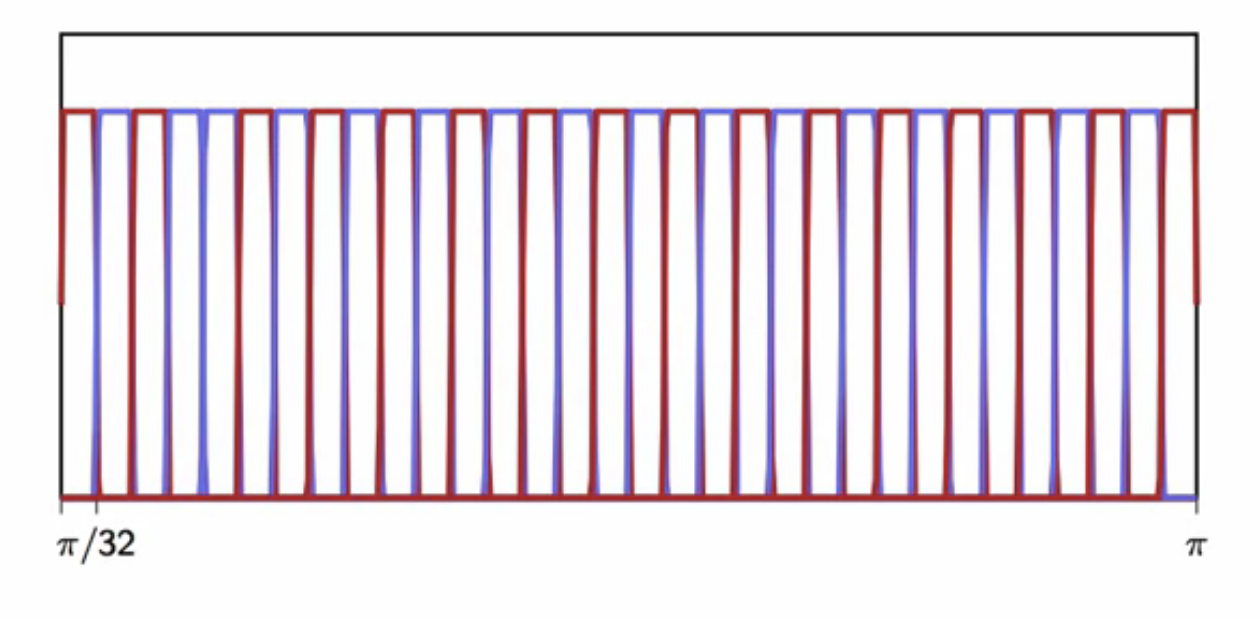
  fig: filter bank spectrum division

• the 32X down-sampler discards 31 out every 32 samples of the output of the filter
  • applied to the output of each modulated filter
  • this is wasteful
  • is made more efficient with optimized sub-band filtering
    • involves some mathematical tricks and your garden variety cleverness

quantization

• step where the bit-rate saving is achieved
• mp3 encoding does uniform quantization of sub-band samples
• number of bits per second in each sub-band is determined by the psycho-acoustic model
• mp3 works on subsequent frames,
  • frame: window of input samples that is processed independently
• one frame
  • 36 samples per band, all quantized by the same quantizer
• rescaling is needed

quantizer

• a quantizer maps an input interval into a set of quantization levels

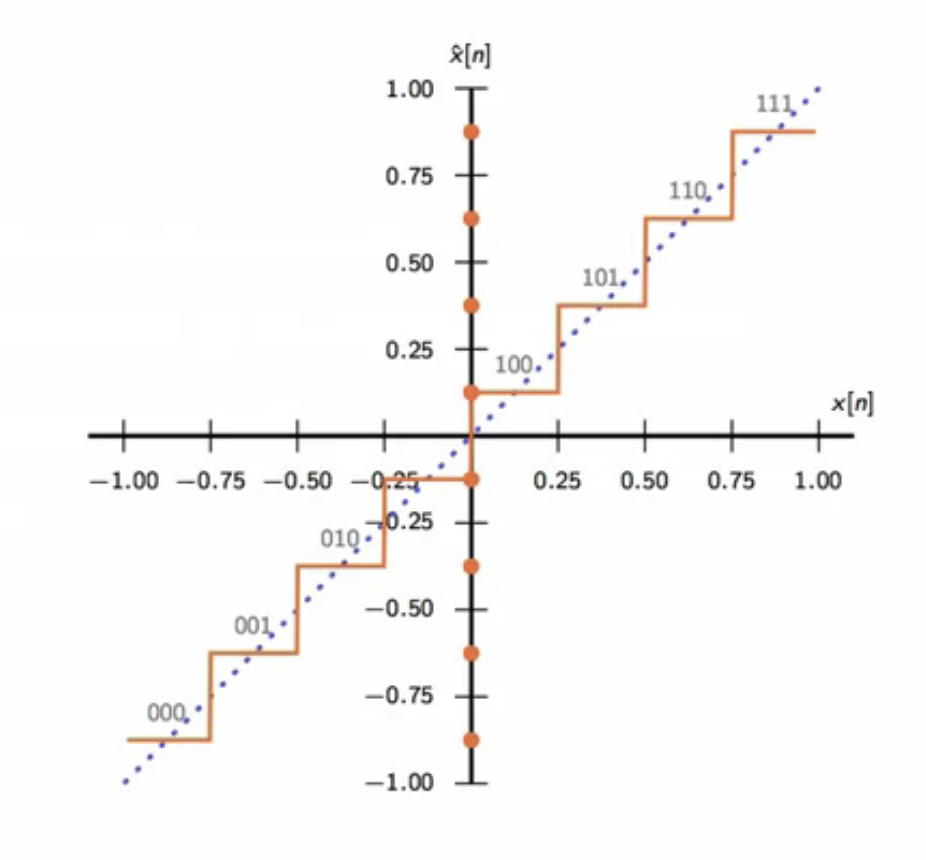
fig: uniform 3-bit quantization function

• the range of the input signal must match the range of the quantizer
• rescaling is done to ensure the full quantization range
  • divide by the largest sample in magnitude
  • the decoder will need the normalization factor along with the quantized data
    • this normalization factor transmission requires 32 bits
• MPEG standard defines 16 scaling factors
  • to aovid transmitting the normalization factor
  • only 4 bits ovehead as opposed to 32 bits for the normalization factor
  • choose the one that best matches the input range

uniform quantizer formula

\[ \tilde{s}[n] = round\Big[ 2^{b-1} (Q_a(b)s[n] + Q_b(b)) \Big] \]

• using b bits from the psycho-acoustic model
• \(Q_a, Q_b\): functions of the number of bits
  • mp3 standard parameters

mp3 performance

• variable bit allocation across sub-bands obtained from the psycho-acoustic model
• to evaluate performance
  • compare original DVD quality audio file
    • uniform bit allocation
    • psycho-acoustic bit allocation

---

references

• ecole - mp3 encoder

---